Треугольной пирамиды развертка для склеивания – Пошаговое решение задачи №4 — Построение развертки призмы и пирамиды и нанесение на нее их линии пересечения

Как построить развертку пирамиды

Развертка поверхности пирамиды — это плоская фигура, составленная из основания и граней пирамиды, совмещенных с некоторой плоскостью. На примере ниже мы рассмотрим построение развертки способом треугольников.

Задача

Пирамиду SABC пересекает фронтально-проецирующая плоскость α. Необходимо построить развертку поверхности  SABC и нанести на нее линию пересечения.

Решение

На фронтальной проекции S»A»B»C» отмечаем точки D», E» и F», в которых след α_v пересекается с отрезками A»S», B»S» и C»S» соответственно. Определяем положение точек D’, E’, F’ и соединяем их друг с другом. Линия пересечения обозначена на рисунке красным цветом.

Определение длины ребер

Чтобы найти натуральные величины боковых ребер пирамиды, воспользуемся методом вращения вокруг проецирующей прямой. Для этого через вершину S перпендикулярно горизонтальной плоскости H проведем ось i. Поворачивая вокруг нее отрезки SA, SB и SC, переместим их в положение, параллельное фронтальной плоскости V.

Действительные величины ребер равны проекциям S»A»₁, S»₁B»₁ и S»C»₁. Отмечаем на них точки D»₁, E»₁, F»₁, как это показано стрелками на рисунке выше.

Треугольник ABC, лежащий в основании пирамиды, параллелен горизонтальной плоскости. Он отображается на ней в натуральную величину, равную ∆A’B’C’.

Порядок построения развертки

В произвольном месте на чертеже отмечаем точку S₀. Через нее проводим прямую n и откладываем отрезок S₀A

0 = S»A»₁.

Строим грань ABS = A₀B₀S₀ как треугольник по трем сторонам. Для этого из точек S₀ и A₀ проводим дуги окружностей радиусами R₁ = S»B»₁ и r₁ = A’B’ соответственно. Пересечение данных дуг определяет положение точки B₀.

Грани B₀S₀C₀ и C₀S₀A₀ строятся аналогично. Основание пирамиды в зависимости компоновки чертежа присоединяется к любой из сторон: A₀

B₀, B₀C₀ или C₀A₀. 

Нанесем на развертку линию, по которой плоскость α пересекается с пирамидой. Для этого на ребрах S₀A₀, S₀B₀ и S₀С₀ отметим соответственно точки D₀, E₀ и F₀. При этом точка D₀ находится на пересечении отрезка S₀A₀ с окружностью радиусом S»D»₁. Аналогично E₀ = S₀B₀ ∩ S»E»₁, F₀ = S₀C₀ ∩ S»F»₁.

развертка. Развертка пирамиды для склеивания. Развертки из бумаги

Хобби 14 июня 2014

Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида — это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.

Материалы и приспособления

Моделирование и выполнение многогранных объемных геометрических фигур — интересный и захватывающий процесс. Из бумаги можно выполнить большое количество всевозможных макетов. Для работы будут необходимы:

• бумага или картон;
• ножницы;
• карандаш;
• линейка;
• циркуль;
• ластик;
• клей.

Определение параметров

Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной треугольной пирамиды.

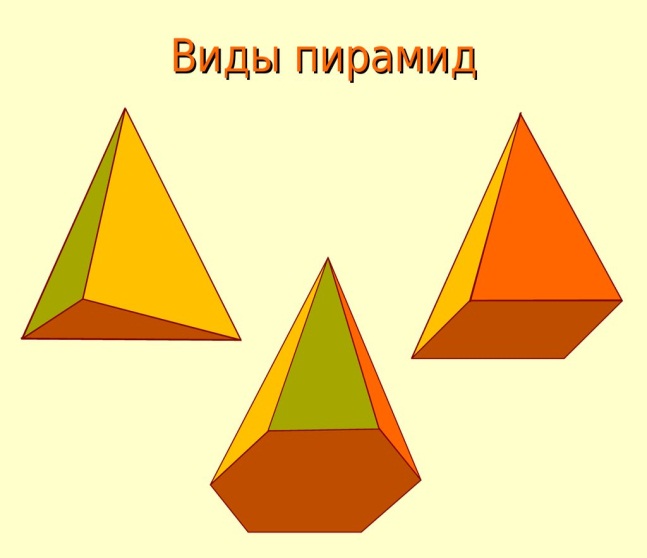
Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием правильный многоугольник, а ее вершина спроецирована в его центр. В качестве основания выбран равносторонний треугольник. Данное условие определяет название. Боковые ребра у пирамиды – это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.

Как выполняется развертка правильной пирамиды?

Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Фигура представляется в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. Правильная пирамида имеет основанием правильный многоугольник, а высота проходит через его центр. Изготавливаем для начала простую модель. В данном случае – это треугольная пирамида. Определяем размеры выбранной фигуры. Чтобы построить развертку пирамиды, основанием которой является правильный треугольник, в центре листа, используя линейку и карандаш, нарисуем основание заданных размеров. Далее к каждой его стороне вычерчиваем боковые грани пирамиды – треугольники. Теперь переходим к их построению. Размеры сторон треугольников боковой поверхности измеряем циркулем. Ножку циркуля ставим в вершину нарисованного основания и делаем засечку. Действие повторяем, перемещаясь в следующую точку треугольника. Пересечение, полученное в результате таких действий, определит вершины боковых граней пирамиды. Их соединяем с основанием. Получаем чертеж пирамиды. Для склеивания объемной фигуры на сторонах боковых граней предусматривают клапаны. Дорисовываем небольшие трапеции.

Сборка макета

Вырезаем ножницами выполненный рисунок по контуру. Аккуратно сгибаем развертку по всем линиям. Клапаны-трапеции заправляем внутрь фигуры таким образом, чтобы ее грани сомкнулись. Их смазываем клеем. Через тридцать минут клей высохнет. Объемная фигура готова.

Развертка четырехугольной пирамиды

Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник. Боковые ребра — треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.

Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.

Завершающий этап выполнения макета

Полученную выкройку фигуры вырезаем по контуру. По начерченным линиям сгибаем бумагу. Сбор объемной фигуры производят путем склеивания. Предусмотренные клапаны смазываем клеем и фиксируем полученную модель.

Объемные макеты сложных фигур

После выполнения простой модели многогранника можно перейти к более сложным геометрическим фигурам. Развертка пирамиды усеченной намного сложнее в выполнении. Ее основаниями являются подобные многогранники. Боковые грани – это трапеции. Последовательность выполнения работы будет такой же, как та, в которой изготавливалась простая пирамида. Развертка будет более громоздкой. Для выполнения чертежа используют карандаш, циркуль и линейку.

Построение чертежа

Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями — подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим окружность, радиусом которой будет измеренное расстояние.

Следующий этап – это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.

Завершение моделирования

Перед склеиванием объемной фигуры чертеж по контуру вырезают ножницами. Далее развертку аккуратно сгибают по начерченным линиям. Крепежные клапаны заправляем внутрь модели. Их смазываем клеем и прижимаем к граням пирамиды. Модели даем высохнуть.

Изготовление разных моделей многогранников

Выполнение объемных моделей геометрических фигур — увлекательное занятие. Чтобы его досконально освоить, следует начинать с выполнения самых простых разверток. Постепенно переходя от простых поделок к более сложным моделям, можно приступать к созданию самых замысловатых конструкций.

Источник: fb.ru

Способ треугольников | Начертательная геометрия

Разверткой многогранника называется плоская фигура, получаемая последовательным совмещением всех граней многогранника с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней – плоских многоугольников.

Способ треугольников используют для построения развертки поверхности пирамиды. Развертка боковой поверхности пирамиды — плоская фигура, состоящая из треугольников — граней пирамиды. Поэтому построение развертки поверхности пирамиды сводится к определению действительной величины ребер пирамиды и построению по трем известным сторонам треугольников — граней пирамиды.

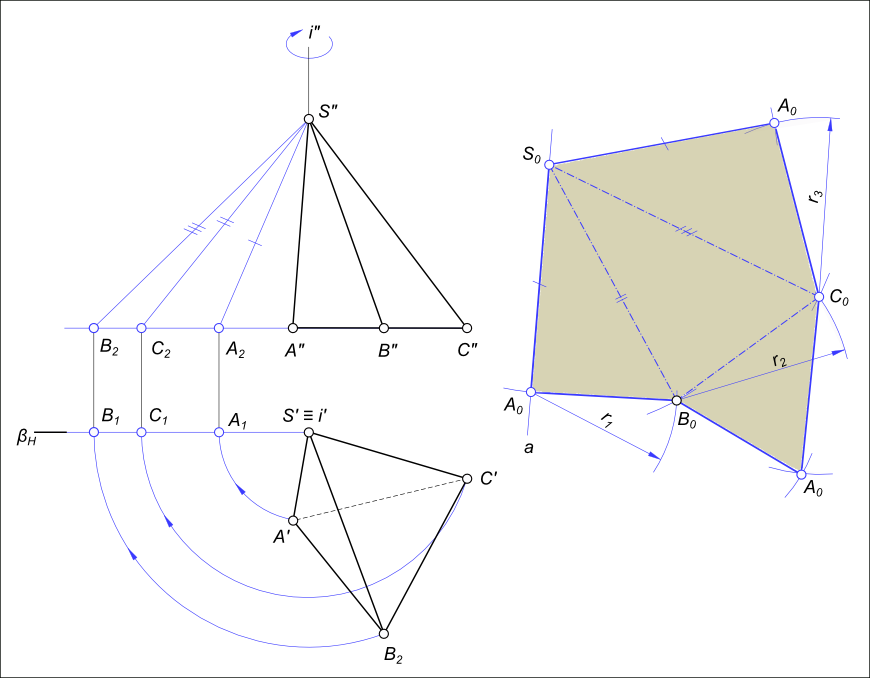
Способ треугольников

Вращаем ребра вокруг оси i (i⊥H и i∋S) и совмещаем с плоскостью β (плоскость β║V β∋i). Выполняем определение действительных величин ребер пирамиды [S»A₂], [S»B₂], [S»C₂]. Приступая к построению развертки проводим произвольную прямую a через произвольную точку S₀. Откладываем на ней от точки S₀ отрезок [S₀A₀]≅ [S»A₂]. Из точки A₀ проводим дугу радиусом r₁=‌A`B`‌, а из точки S₀ — дугу радиусом R₁=‌S»B₂. Пересечение дуг укажет положение вершины B₀ ΔS₀A₀B₀ (ΔS₀A₀B₀≅ΔSAB — грани пирамиды). Аналогично определяем положение точек C₀ и A₀. Соединяя точки A₀B₀C₀A₀S₀, получим развертку боковой поверхности. Присоединив к какой-либо стороне (ребру) основание (ΔABC) — получаем полную развертку поверхности пирамиды SABC.

Способ треугольников использован для построения развертки поверхности усеченной пирамиды в графической работе №12: Графическая работа 12

+

Развёртки многогранников. Методический материал для конструирования пространственных фигур.

Развёртки геометрических объёмных тел

На плотной бумаге начертите подобную развёртку, вырежьте, аккуратно склейте.

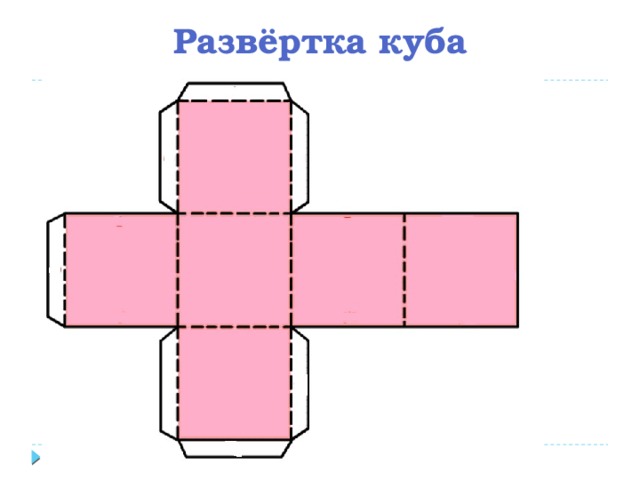
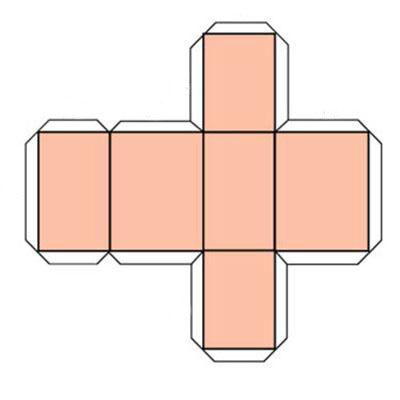
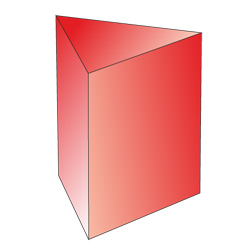
Треугольная призма

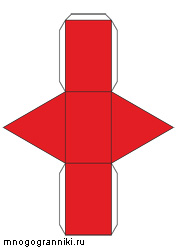
Четырёхугольная призма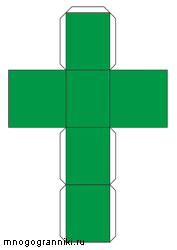

Пятиугольная призма

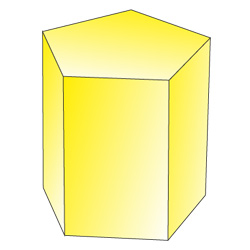
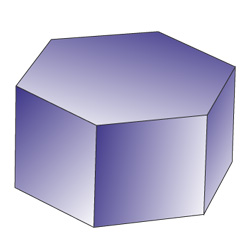
Шестиугольная призма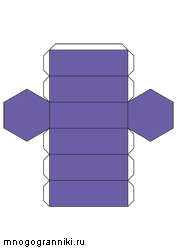

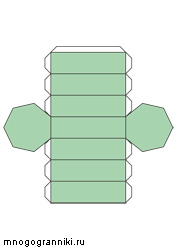
Семиугольная призма

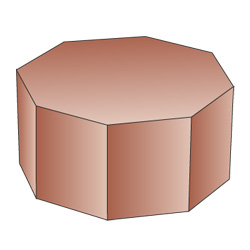
Восьмиугольная призма

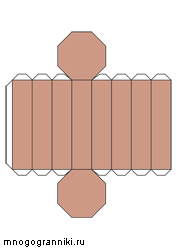
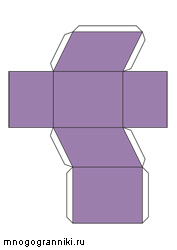
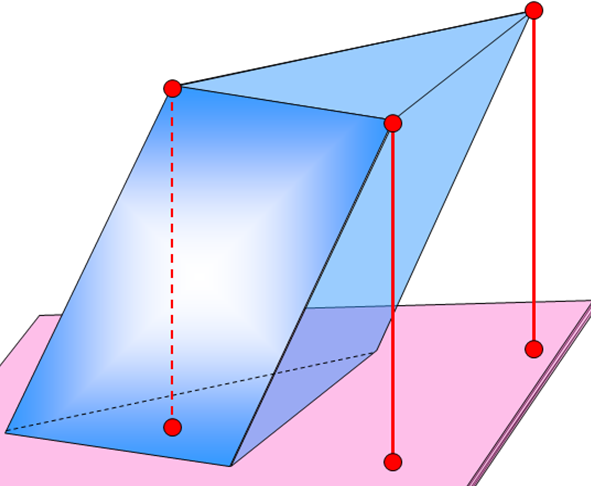
Наклонный параллелепипед

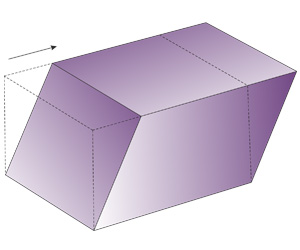
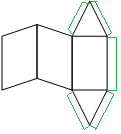
Наклонная треугольная призма

Цилиндр

Конус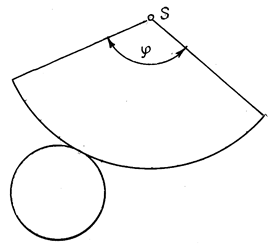

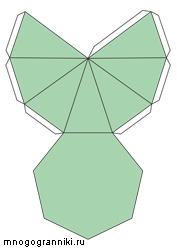
Пирамида

Усечённый цилиндр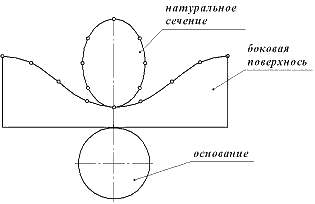

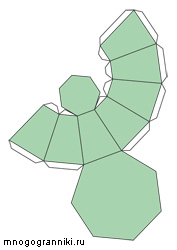
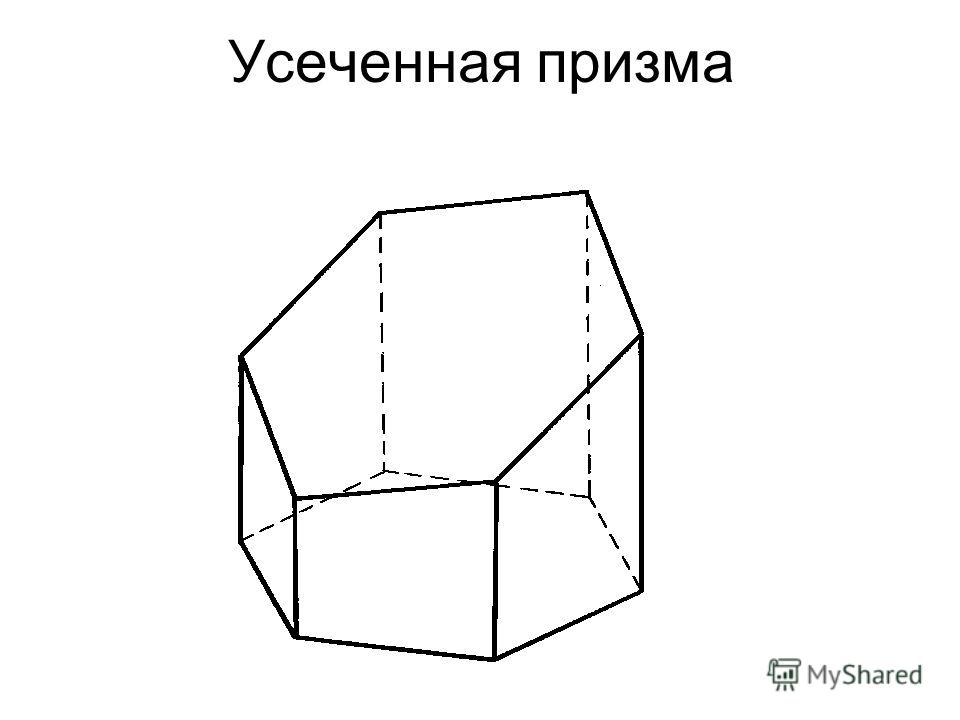
Усечённая пирамида

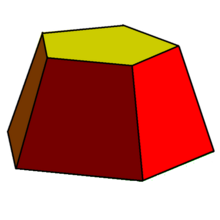
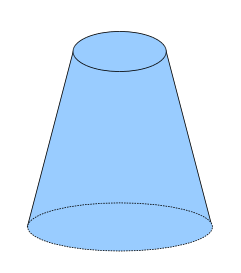
Усечённый конус

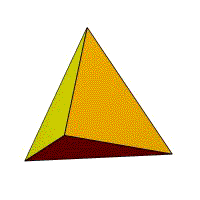
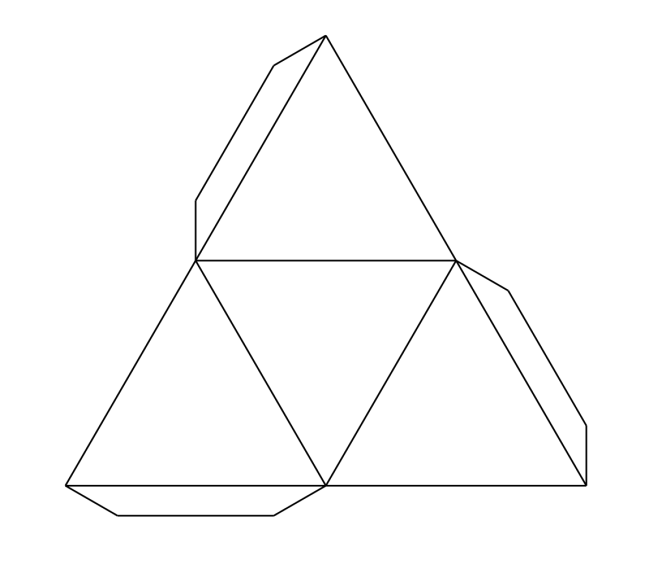
Тетраэдр

Октаэдр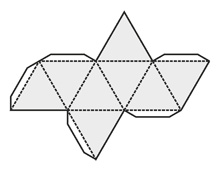

Икосаэдр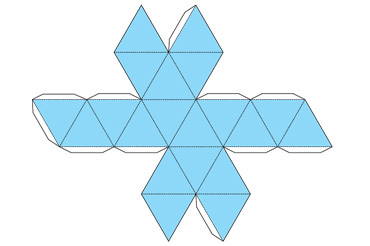

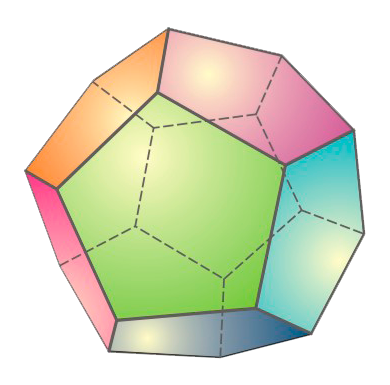
Додекаэдр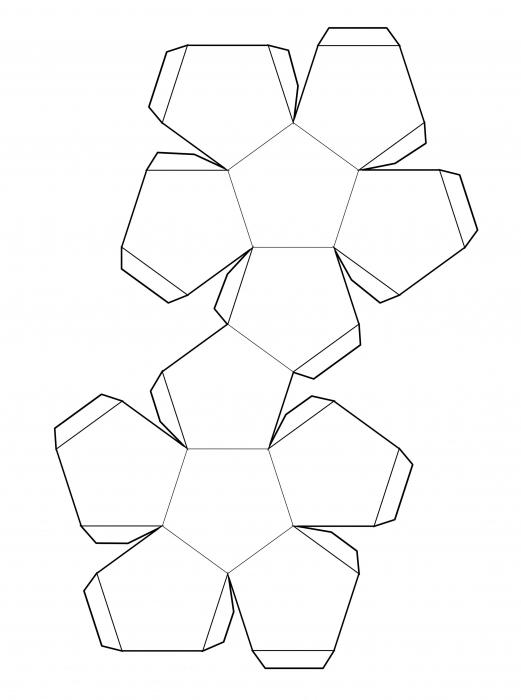

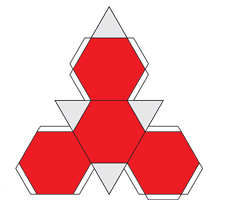
Усечённый тетраэдр

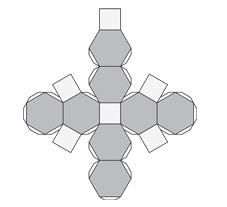
Усечённый октаэдр

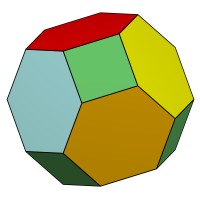
Усечённый куб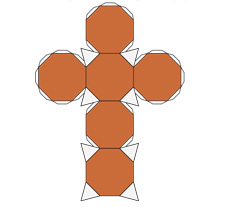

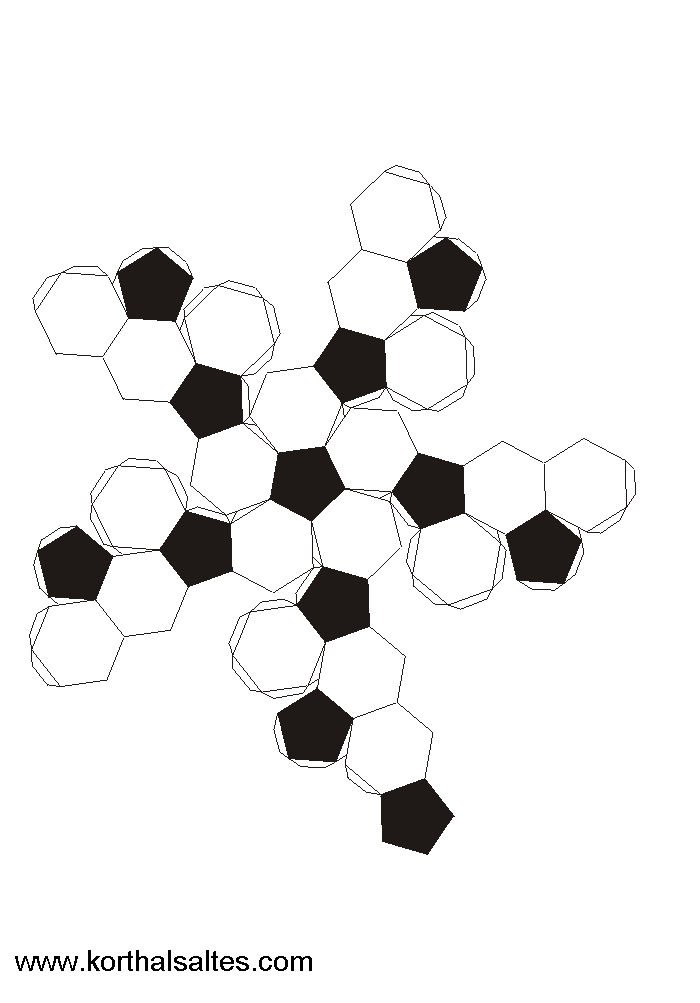
Усечённый икосаэдр

Усечённый додекаэдр

Кубооктаэдр

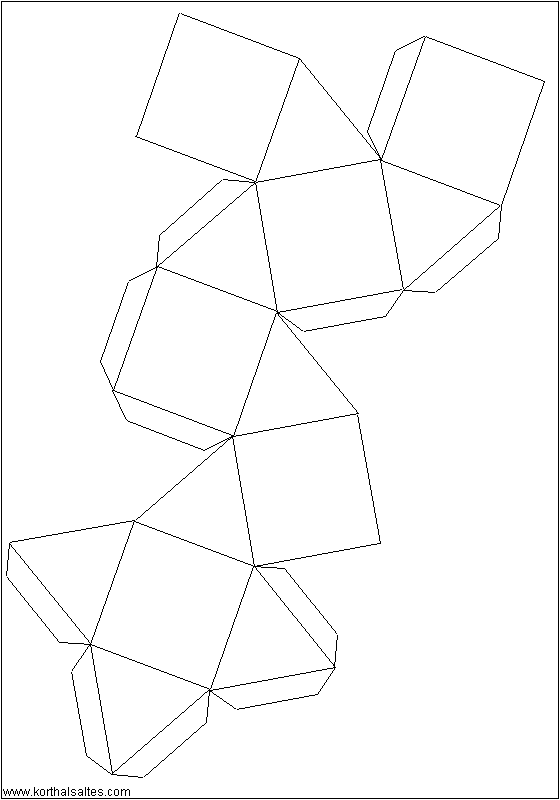
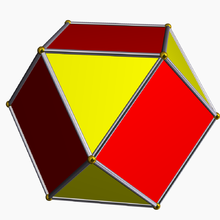
Икосододекаэдр

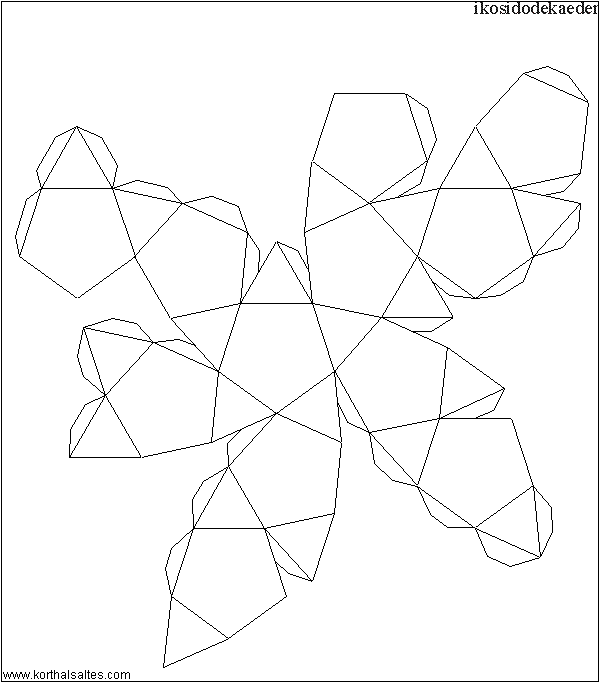
Ромбокубооктаэдр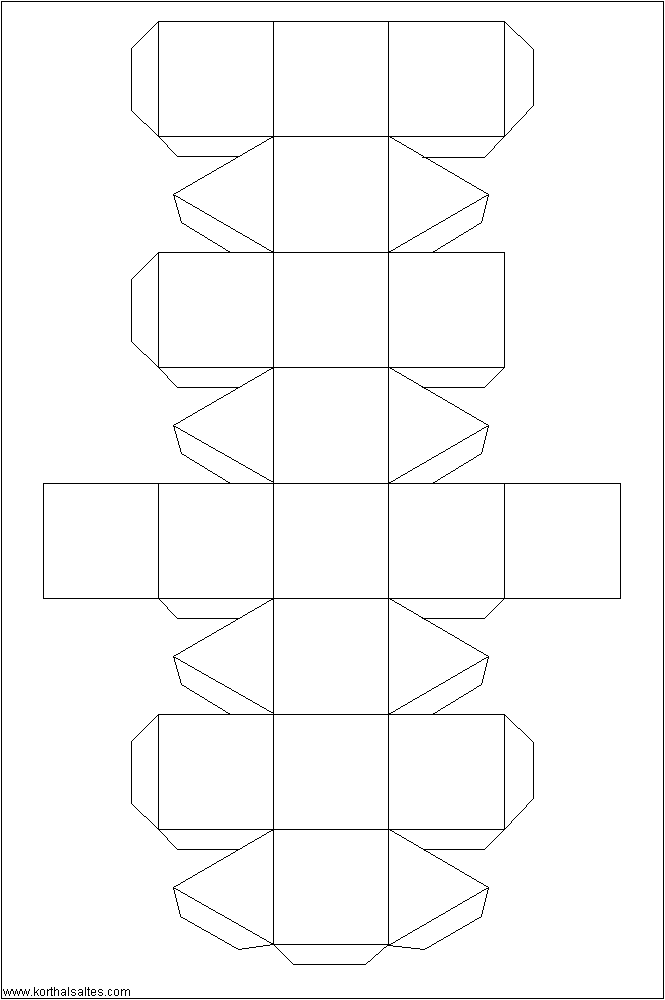

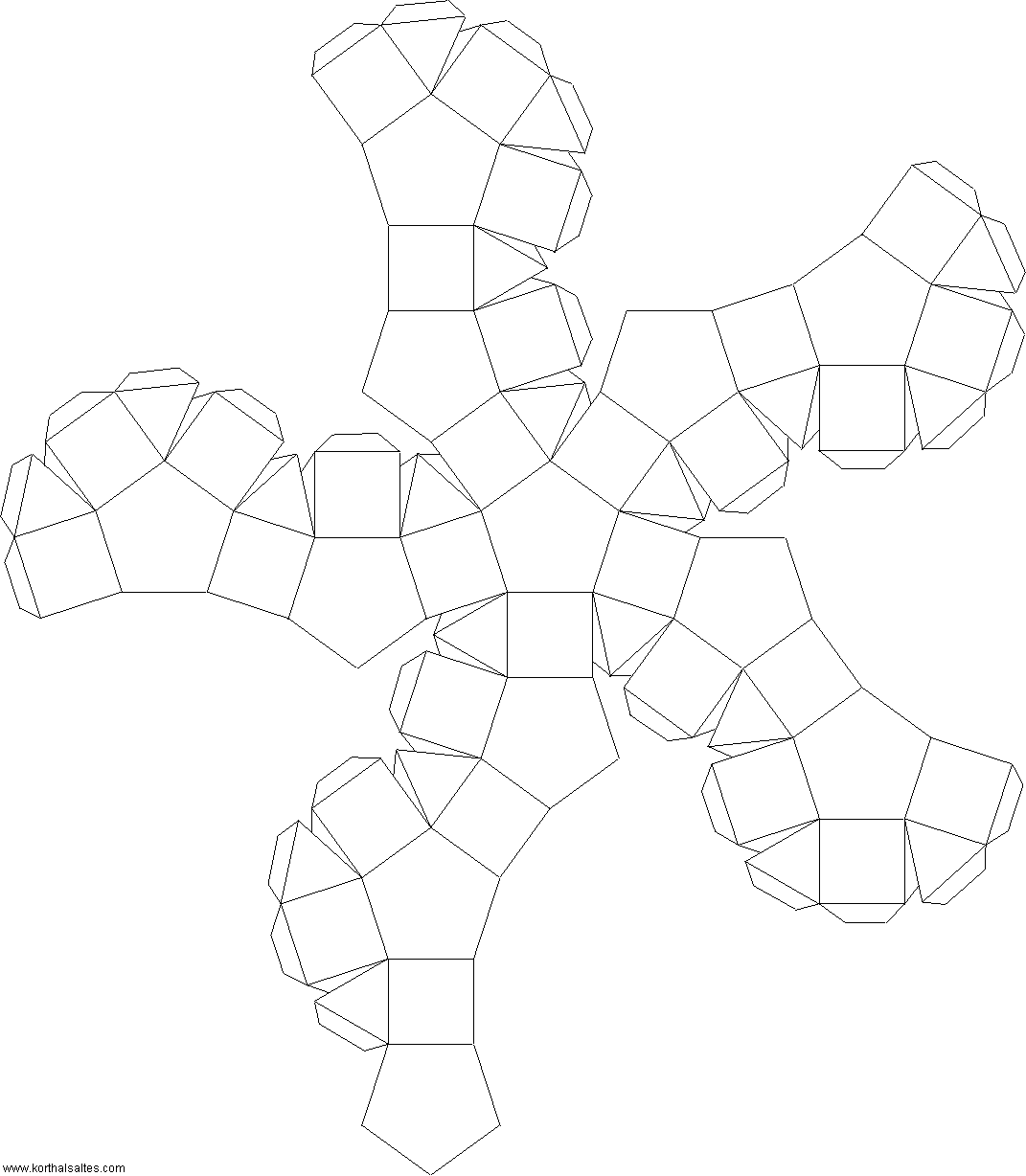
Ромбоикосододекаэдр

Ромбоусечённый

кубооктаэдр

Ромбоусечённый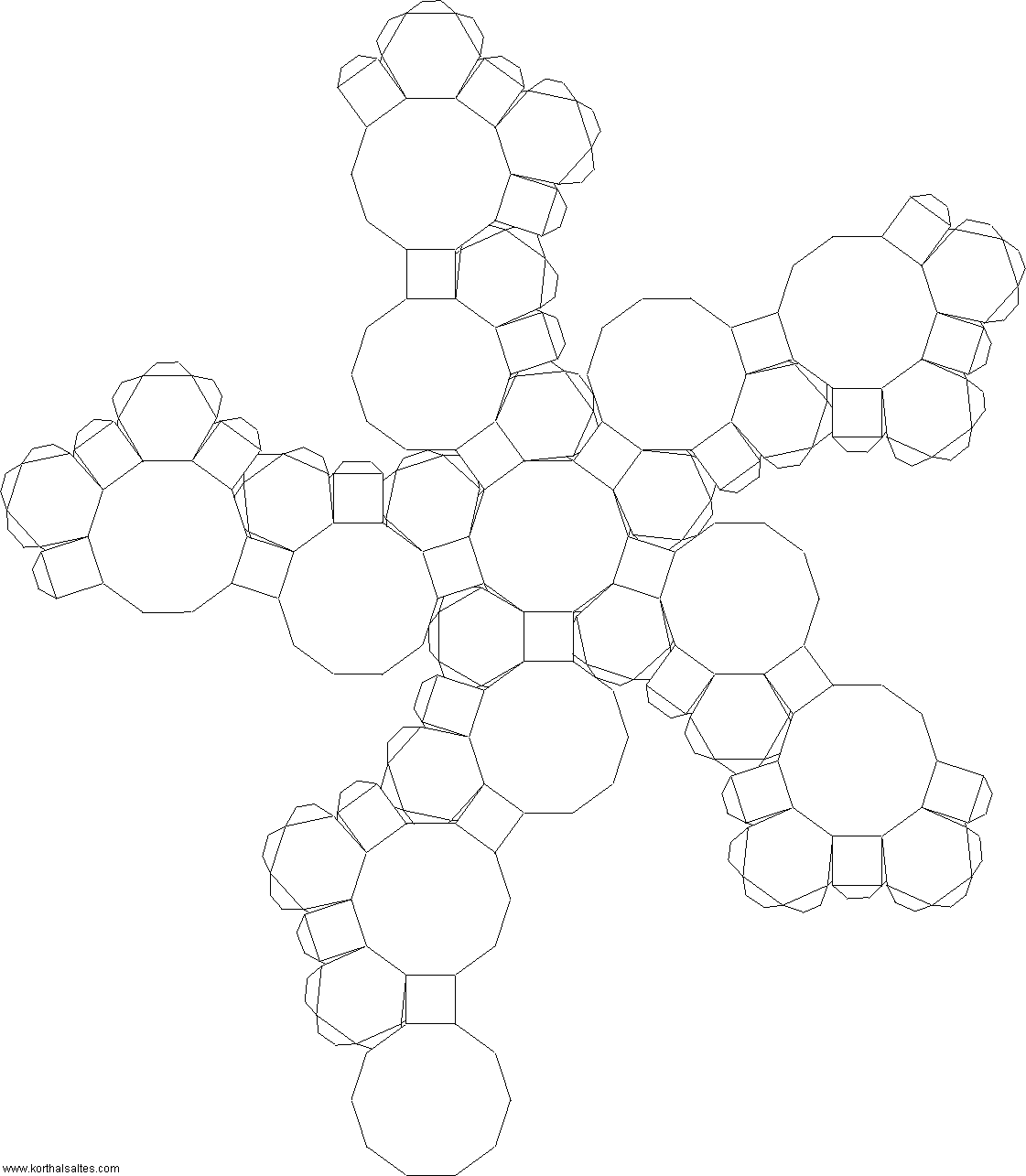

икосододекаэдр

Курносый куб

Курносый додекаэдр

Звёздчатый октаэдр

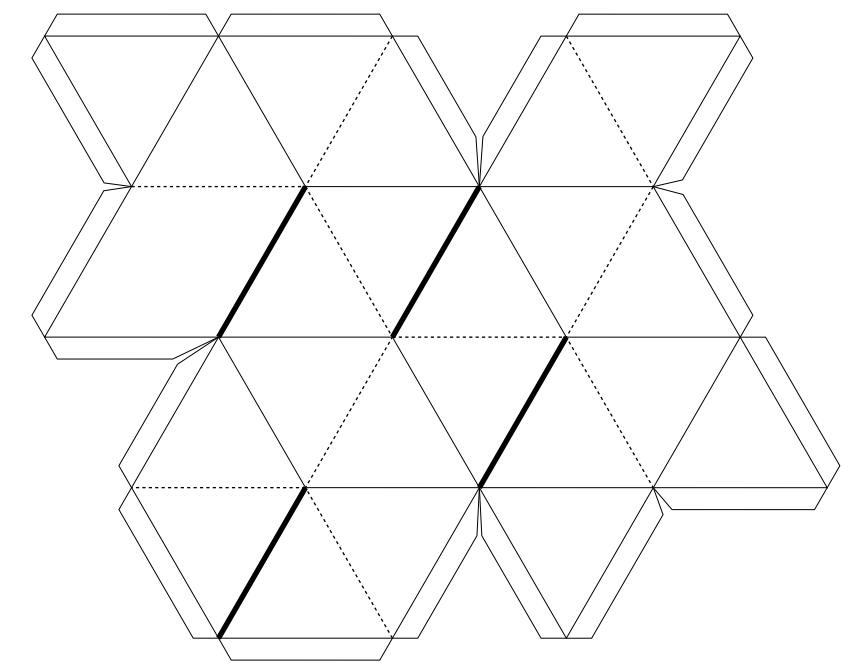
Малый звёздчатый

додекаэдр

Большой додекаэдр

Состоит из 4-х деталей, причем детали под номерами № 3 и 4 — по одной штуке,

а № 1 и 2 — по две штуке

Развертка состоит из прямоугольных треугольников,   включает в себя еще  и клапаны.

Согнуть развертку по всем необходимым линиям.  

на схеме треугольнички, составляющие звездочку, выделены «крестиками»

Большой звёздчатый додекаэдр:

клеим пирамидки соответствующего размера на додекаэдр

Соединение пяти октаедров

Развертка треугольной пирамиды для склеивания — kak.floatcamera.ru

Вообще пирамиду довольно просто можно нарисовать. Для начала лист необходимо разделить пополам, это можно сделать линией, использовав линейку. Дальше рисуем боковые части пирамиды и все готово.

Все легко и просто рисуется!!

В школе мы все рисовали пирамиды на уроках,только это были геометрические фигуры.И для того,чтобы нарисовать пирамиду,вам обязательно будет нужна линейка и карандаш,запаситесь ластиком,чтобы стирать ненужное.

Пирамида должна выглядеть вот таким образом:



И чтобы ее нарисовать,мы должны для начала нарисовать квадрат,затем провести грани внутри квадрата и соединить их у основания.Зеленым цветом выделены линии на основании пирамиды, для их последующего соединения.



Потом вы можете раскрасить вашу пирамиду в любой цвет.Для этого подойдут либо краски,либо цветные фломастеры.И ваша пирамида будет симпатичнее в цвете.

Вот видео мастер-класс как нарисовать пирамиду Хеопса вместе со Сфинксом.

А ниже приведено поэтапное рисование пирамиды, при желании можно нарисовать песок и пустить караван верблюдов и загадочная Долина фараонов готова:)













• Содержание статьи:

  Рисуем пирамиду поэтапно

  Я конечно не художник и мне обьяснить как правильно рисовать пирамиду сложно, но я могу показать пошагово, как рисуют мастера.

  Думаю, что пирамиду нарисовать труда не составляет, глядя на эти эскизы.

  

  

  

  

Рисуем рисунок пирамиды. Сделаем это мы за семь шагов.

Первый шаг. Нарисуем квадрат, длина его стороны будет равна пяти сантиметров.



Второй шаг. Берем циркуль, выставляем его длину равную стороне квадрата. Теперь ставим иглу циркуля в самую крайнею правую точку и проводим линию из противоположного края до верхней стороны, как показано на рисунке:



Третий шаг. Делаем аналогичную операцию из противоположного края, таким образом, у нас получились две кривые, пересекшиеся в одной точке.



Четвертый шаг. Из обеих крайних точек основания проводим две прямые пересекающиеся в точке пересечения кривой.



Пятый шаг. Стираем кривые линии и боковые и верхние стороны квадрата.



Шестой шаг. Рисуем боковую сторону пирамиды:





Нарисовать пирамиду карандашом, наверное, одно из самых легких задач, связанных с рисованием. Здесь не нужен какой-то особый талант или обладание какини либо навыками рисования. Предосатвляю, поучительное видео.

Нарисовать пирамиду карандашом поэтапно можно, опираясь на следующие схемы:





Этапы рисования пирамид:

1) Начинаем делать наброски;

2) Начинаем прорисовывать элементы как на рисунках;

3) Переходим к детализации изображения;

4) Штрихуем и обводим по контуру.

Пирамиды являются памятниками культуры Египта и мировой культуры в целом.

В древнем Египте пирамиды были местом, куда погребались фараоны. И многие из них (пирамид) носили/носят имя фараонов, которые были погребены в ней. (Хеопс, Тутанхамон).

Сейчас же, именно ради них многие и едут в Египет. Чтобы посмотреть на великолепные сооружения древних времен.

А вот как нарисовать пирамиды карандашом поэтапно :

Шаг первый:



Шаг второй:



Шаг третий:



Шаг четвертый:



Чтобы изобразить пирамиду, нужно нарисовать два прилегающих друг к другу треугольника, например, как в видео ниже. А если необходима египетская пирамида, то нужно добавить рисунок наподобие кирпичной кладки на пирамиде и дорисовать вход.

Прямоугольник, квадрат, треугольник, трапеция и другие — геометрические фигуры из раздела точной науки. Пирамида — это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.

Материалы и приспособления

Моделирование и выполнение многогранных объемных геометрических фигур — интересный и захватывающий процесс. Из бумаги можно выполнить большое количество всевозможных макетов. Для работы будут необходимы:

• бумага или картон;
• ножницы;
• карандаш;
• линейка;
• циркуль;
• ластик;
• клей.

Определение параметров

Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной

Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием а ее вершина спроецирована в его центр. В качестве основания выбран Данное условие определяет название. Боковые ребра у пирамиды — это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.

Как выполняется развертка правильной пирамиды?

Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Фигура представляется в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. имеет основанием правильный многоугольник, а высота проходит через его центр. Изготавливаем для начала простую модель. В данном случае — это треугольная пирамида. Определяем размеры выбранной фигуры.

Чтобы построить развертку пирамиды, основанием которой является правильный треугольник, в центре листа, используя линейку и карандаш, нарисуем основание заданных размеров. Далее к каждой его стороне вычерчиваем боковые грани пирамиды — треугольники. Теперь переходим к их построению. Размеры сторон треугольников боковой поверхности измеряем циркулем. Ножку циркуля ставим в вершину нарисованного основания и делаем засечку. Действие повторяем, перемещаясь в следующую точку треугольника. Пересечение, полученное в результате таких действий, определит вершины боковых граней пирамиды. Их соединяем с основанием. Получаем чертеж пирамиды. Для склеивания объемной фигуры на сторонах боковых граней предусматривают клапаны. Дорисовываем небольшие трапеции.

Сборка макета

Вырезаем ножницами выполненный рисунок по контуру. Аккуратно сгибаем развертку по всем линиям. Клапаны-трапеции заправляем внутрь фигуры таким образом, чтобы ее грани сомкнулись. Их смазываем клеем. Через тридцать минут клей высохнет. Объемная фигура готова.

Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник. Боковые ребра — треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.

Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.

Завершающий этап выполнения макета

Полученную выкройку фигуры вырезаем по контуру. По начерченным линиям сгибаем бумагу. Сбор объемной фигуры производят путем склеивания. Предусмотренные клапаны смазываем клеем и фиксируем полученную модель.

Объемные макеты сложных фигур

После выполнения простой модели многогранника можно перейти к более сложным геометрическим фигурам. Развертка пирамиды усеченной намного сложнее в выполнении. Ее основаниями являются подобные многогранники. Боковые грани — это трапеции. Последовательность выполнения работы будет такой же, как та, в которой изготавливалась простая пирамида. Развертка будет более громоздкой. Для выполнения чертежа используют карандаш, циркуль и линейку.

Построение чертежа

Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями — подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим которой будет измеренное расстояние.

Следующий этап — это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники — квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.

Завершение моделирования

Перед склеиванием объемной фигуры чертеж по контуру вырезают ножницами. Далее развертку аккуратно сгибают по начерченным линиям. Крепежные клапаны заправляем внутрь модели. Их смазываем клеем и прижимаем к граням пирамиды. Модели даем высохнуть.

Изготовление разных моделей многогранников

Выполнение объемных моделей геометрических фигур — увлекательное занятие. Чтобы его досконально освоить, следует начинать с выполнения самых простых разверток. Постепенно переходя от простых поделок к более сложным моделям, можно приступать к созданию самых замысловатых конструкций.

Одно из величайших чудес мира — пирамиды Египта, сохранились до наших дней. Более того, каждый год множество туристов отправляются в Гизу лишь для того, чтобы увидеть пирамиды и Сфинкса, который как будто охраняет сооружения, неподвижно застыв среди руин древнего храма.

Чтобы заинтересовать ребенка, можно рассказать ему следующее:

• До сих пор никто не знает, каким образом и для чего были построены пирамиды. Ученые выяснили, что это чудо света было построено намного раньше, чем появилось Египетское царство.
• Несмотря на то, что в древние времена не было современной техники, пирамиды построены с математической точностью.
• На протяжении трех тысяч лет пирамида фараона Хеопса была самым высоким сооружением в мире.

Нарисовать пирамиды очень просто. Следите за нашей инструкцией и у вас все получится. Вам понадобятся: лист бумаги; карандаш; ластик; линейка;
Шаг 1

Место для пирамид

Для начала рисуем прямоугольник, в котором будем размещать пирамиды. Чтобы облегчить процесс, можете воспользоваться линейкой.
Далее делим прямоугольник на три части. У вас должны получиться два прямоугольника слева и справа, а в центре квадрат, немного больше, чем прямоугольники.

Шаг 2

Первая пирамида

На этом этапе начинаем рисовать пирамиды. Для начала изображаем пирамиду в первом прямоугольнике. Ее еще называют пирамидой Хефрена. Она вторая по величине и находится перед остальными. Заметьте, что часть треугольника выходит за прямоугольник.

Шаг 3

Вторая пирамида

Пришла очередь Великой или пирамиды Хеопса. Она начинается в первом прямоугольнике и выходит за грани второго. Верх треугольника касается верхней стороны квадрата.

Шаг 4

Третья пирамида

Последняя пирамида фараона Микерина самая маленькая. Ее мы рисуем только в прямоугольнике, не выходя за грани. Часть этого сооружения спрятано за Великой пирамидой.

Шаг 5

Убираем лишние линии

Теперь нужно стереть все ненужные линии. Остаются лишь пирамиды. Полностью нарисована только первая, так как остальные спрятаны друг за другом.

Шаг 6

Рисуем кирпичи

От верхушек пирамид проводим прямые линии вниз, обозначая углы.
По всей первой пирамиде проводим горизонтальные линии.
Эти линии через небольшие промежутки разделяем вертикальными линиями, обозначая кирпичи.
Рисуем горизонтальные линии на оставшихся пирамидах.
Аналогично разделяем линии, чтобы получились кирпичи.

В этом уроке создадим рисунок пирамиды. Эта фигура из разряда легких, пожалуй, легче чем куб. Если вы внимательно прочитали , то этот урок для вас будет больше повторение пройденного материала. Еще раз хочу повторить, что изобразительное искусство начинается с , или пером, или ручкой… и с натуры.

Здесь мы просмотрим больше схематическое создание пирамиды, чем художественное. Вообще наши уроки больше схемы рисунков, но понять принцип рисунка можно.

А увидеть создание рисунка в реальном времени, правда это рисунок не пирамиды, а , можно посмотреть на нашем сайте.

Таким рисунок должен быть по окончании нашего урока. Все картинки кликабельны:

Рисунок пирамиды в картинках

В уроке я показывал, как выстроить ее в пространстве, правда там мы строили фигуру с одной точкой схода. Здесь она построена с двумя точками схода:

Вначале строим каркас пирамиды. Рисунок внизу:

Теперь обозначим тень:

У нас три основных плоскости A — передняя часть пирамиды (свет). B — боковая часть, находящаяся в тени (собственная тень пирамиды). C — (падающая тень). Смотрим вниз:

Заливаем плоскость A тоном. Рисунок внизу:

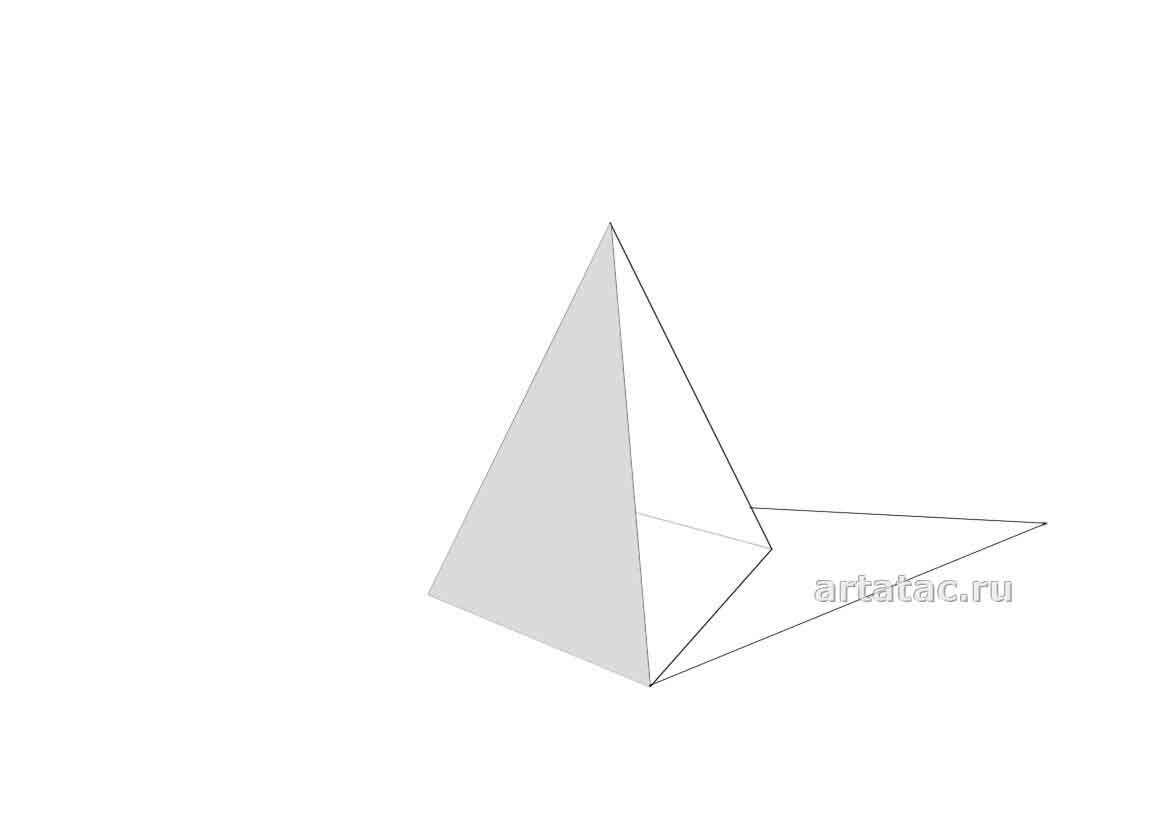
Плоскость B , находится в тени, естественно она темнее света плоскости A . Так и сделаем:

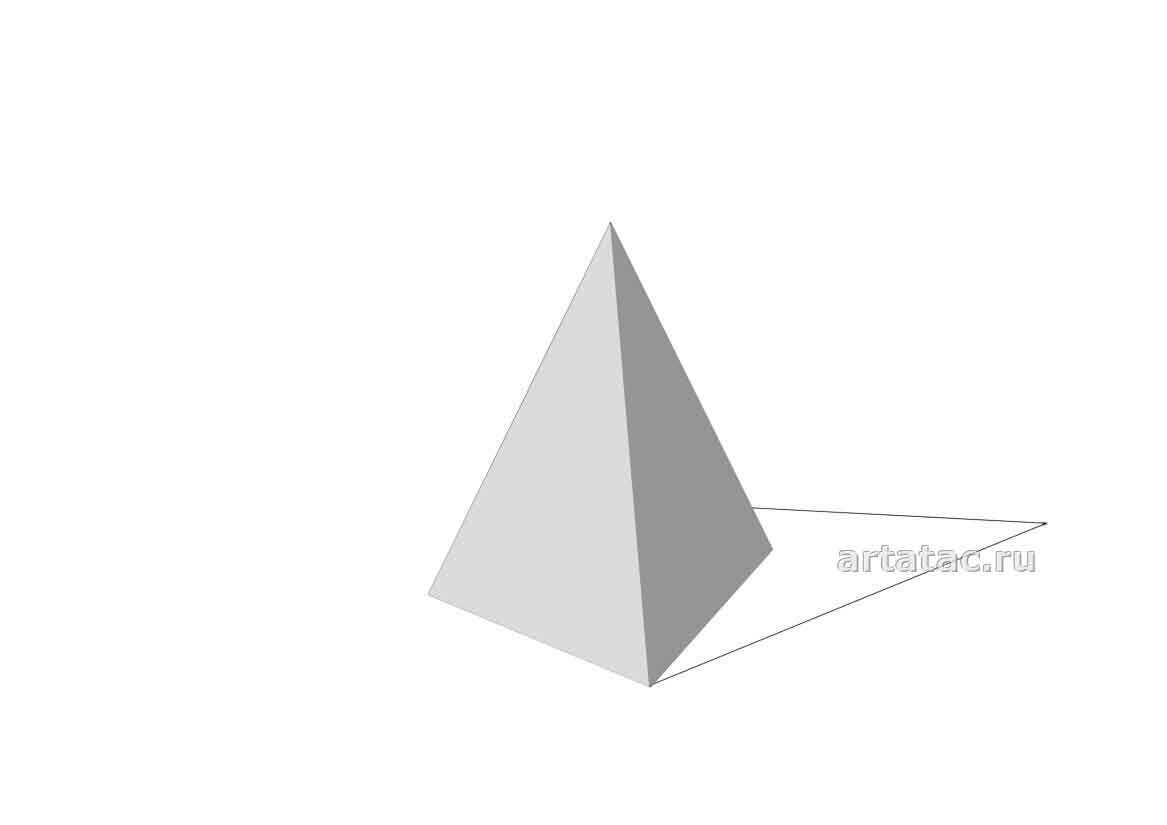
А вот самая темная это падающая тень C . Поэтому, как вы правильно догадались, зальем ее самым темным тоном. Смотрим вниз:

Далее прорисуем нашу пирамиду. На границе соприкосновения плоскостей A и B , край плоскости B затемним. Также затемним тень C ближе к нам, и тень на соприкосновении плоскостей C и B . Немного осветлим сзади плоскость B , где она соприкасается с тенью C , это осветление называется РЕФЛЕКС (отражение от плоскости, на которой стоит наша пирамида). Смотрим вниз:

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Источник: zvdom.ru

Читайте также

Правильная пирамида развертка | МеханикИнфо

Правильная пирамида развертка. 4.14/5 (82.86%) проголосовало 7

 

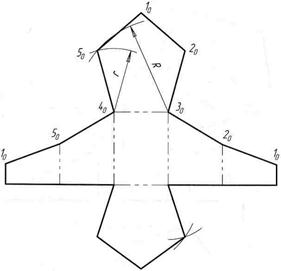
Правильная пирамида. имеющая в основании правильный n — угольник (в данном случае шестиугольник), показана на рис. 1. Для удобства построения одно из ребер, например O’V’ расположено в плоскости, параллельной фронтальной проекции.

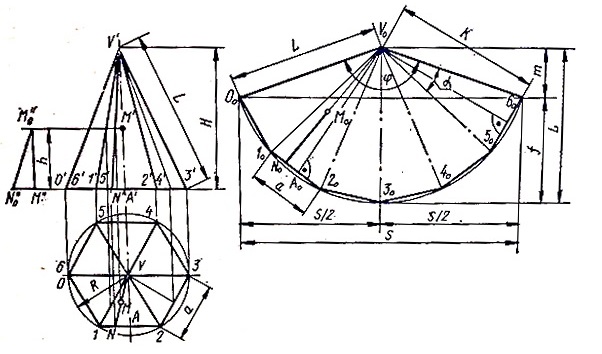
Рис. 1. Правильная пирамида развертка.

Поэтому на рисунке показана его натуральная величина. Построение развертки боковой поверхности следует начинать с произвольной точки V₀, из нее как из центра радиусом, равным длине бокового ребра пирамиды R = L, описывается дуга. От произвольной точки O₀ на дуге n раз последовательно откладывается сторона многоугольника. Полученные точки 0₀, 1₀, …, 6₀ последовательно соединяются между собой и с высотой V₀.

 

Если дана точка М, принадлежащая одной из плоскостей пирамиды, то ее можно перенести на развертку следующим образом. Проводится прямая MV до пересечения со стороной основания в точке N и соответственно М’V’ до пересечения в точке N’. Расстояние 1N откладывается от точки 1₀ на стороне 1₀2₀ развертки до точки N₀. Проводится прямая N₀V₀. Для определения действительной длины отрезка NM нужно построить вспомогательный прямоугольный треугольник со сторонами N”₀M” = NM и М”М”₀ = h. От точки N₀ откладывается расстояние N”₀M”₀. Получаем точку М₀.

Рис. 2. Правильный пятиугольник усеченный плоскостью.

Для аналитического определения элементов разверток пирамиды используют ряд зависимостей; боковое ребро ,

высота треугольников, составляющих развертку боковой поверхности ; тангенс половины плоского угла при вершине пирамиды:

полный угол развертки ᵠ = nα.

Величины s, m и f можно определить, воспользовавшись зависимостями:

;

.

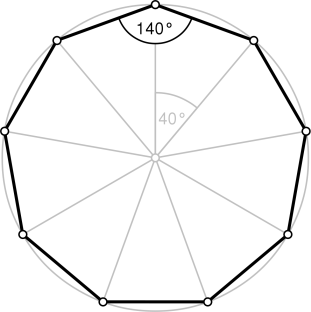
Для четного количества плоскостей пирамиды (рис. 1):

.

Для нечетного количества плоскостей пирамиды (рис. 2):

.